DEFLESSIONE MAGNETICA

CAMPO MAGNETICO TRA LE DUE BOBINE DI HELMOTZ

Per impostare le bobine di Helmholtz, due bobine simili con raggio R sono posizionate alla stessa distanza R. Quando le bobine sono collegate in modo tale che la corrente attraverso le bobine scorra nella stessa direzione, le bobine di Helmholtz producono una regione con un campo magnetico uniforme.

Utilizzando l'equazione ricavata dalla legge di Biot-Savard, quando si ha una campo magnetico nella direzione orizzontale e una bobina con solo un avvolgimento:

B(x) = μ0 ⋅ V ⋅  R^2/2 (R^2 + y^2)^3/2

Poiché in questo caso il campo magnetico si calcola con:

Come si muovono gli elettroni all'interno del campo magnetico?

Un cannone ad elettroni produce un fascio di elettroni, questo fascio è perpendicolare al campo magnetico delle bobine di Helmholtz e il gas Neon rende la traiettoria degli elettroni visibili.

Ipotesi

In particolar modo l'intensità di corrente I, tra le bobine di Helmholtz influisce sul raggio del fascio di elettroni; infatti, all'aumentare di essa diminuisce il raggio dell'orbita circolare.

La tensione di accelerazione Va influisce anch'essa sul raggio del fascio di elettroni, infatti, all'aumentare di essa aumenta il raggio dell'orbita circolare

Analisi dei dati

Andiamo ora ad analizzare quali forze agiscono sugli elettroni nel campo elettrico tra le due bobine.

La forza di Lorentz agisce all'interno del campo magnetico muovendo le cariche: Florentz = q ⋅ V0 ⋅ B

poiché gli elettroni si muovono sempre perpendicolarmente al campo magnetico e la carica q è la carica dell'elettrone, l'equazione si può semplificare con:

FLorentz = e ⋅ V0 ⋅ B

Sapendo che la forza centripeta è uguale a Fc = m ⋅ V0^2/r

Poiché le due forze si equivalgono possiamo paragonarle:

FLorentz = Fc

e ⋅ v0 ⋅ B = m ⋅ v0^2/r

isolando il raggio ricaviamo che:

r = m ⋅ v0/e ⋅ B

RICERCA DELLA CARICA DI UN ELETTRONE

Storia

Thomson ha cercato di sviluppare affermazioni quantitative.

Nel 1890 la conoscenza degli elettroni era limitata, persino la parola elettrone era poco conosciuta.

Nonostante ciò, Thomson, grazie ad un esperimento, ha scoperto che:

Florentz = Fc

e ⋅ v0 ⋅ B = m ⋅ v0^2/r

e ⋅ B = m ⋅ v0/r

Sostituendo poi v0 con una quantità misurabile nell'esperimento, per fare ciò utilizziamo il principio di conservazione dell'energia meccanica: il lavoro eseguito nel campo E corrisponde all'energia cinetica

e ⋅ Va = ½ ⋅ m ⋅  v0^2

v0 = √(2 ⋅ e ⋅ Va/m)

Sostituendo v0 e elevando al quadrato ricaviamo

e^2 ⋅ B^2 = m^2 ⋅ 2 ⋅ e ⋅ Va/r^2

Isolando e/m ricaviamo

e/m = 2 ⋅ Va/(B ⋅ r)^2

Thomson è stato in grado di determinare il rapporto di massa e carica di un elettrone, tale rapporto è chiamato carica specifica di una particella.

Rapporto tra carica e massa elettronica

Sulla base dello studio del movimento degli elettroni nei campi magnetici é possibile determinare la carica specifica dell'elettrone:

L'equilibrio delle forze Florentz = Fc può essere determinato come:

e/m = v0/r ⋅ B

Sostituiamo v0 con la formula:

v0 = √2 ⋅ e/m ⋅ Va

Eleviamo al quadrato e isoliamo e/m ottenendo quindi

e/m = 2 ⋅ Va/(B ⋅ r)^2

La tensione di accelerazione Va può essere modificata nell'esperimento, il campo magnetico B può essere calcolato e mostrato con la formula:

B = μ0 ⋅ 8 ⋅ I ⋅ N/√125 ⋅ R

B è direttamente proporzionale all'intensità corrente I variabile della bobina.

Il raggio r della traiettoria deve essere determinato sperimentalmente, per farlo si può prendere come esempio questa tabella

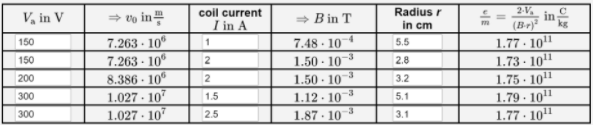
Quindi l'esperimento ottiene che e/m corrisponde a (1,76+-0,03) 10^11 C/kg

Il valore reale corrisponde a 1,75882 10^11 C/kg

Traiettoria degli elettroni con un angolo α rispetto al campo magnetico

Ruotando il tubo catodico, si può osservare la variazione della traiettoria del fascio di elettroni a causa della presenza di un angolo α diverso da 90 gradi. Infatti, posto che il vettore velocità degli elettroni non è più perpendicolare al campo magnetico, si può osservare come la traiettoria (compiuta dallo stesso fascio di elettroni) sia di forma elicoidale. Questo è dovuto alla presenza delle 2 componenti della velocità: quella perpendicolare al campo magnetico e quella parallela.

Prendendo un valore costante del campo magnetico, possiamo osservare i differenti valori Va1 = 125V; Va2 = 175V; Va3 = 300V.

Invece, fissando il valore di Va, si hanno i seguenti valori di intensità della corrente elettrica I1 = 2A, I2 = 2,5A, I3 = 5A

Vista matematica della traiettoria

Considerando v0 il vettore velocità degli elettroni, si possono quindi individuare le due componenti vx(v parallela) e vy(v perpendicolare). Pertanto, nominando α l'angolo tra la velocità degli elettroni e il campo magnetico, si ha che: vx= v0 ⋅ cos(α) e vy = v0 ⋅ sin(α).

Componente della velocità perpendicolare a B

Andando ad analizzare il moto degli elettroni, vale ancora l'uguaglianza tra la forza di Lorentz e la forza centripeta degli elettroni.

F Lorentz = Fcentripeta

e ⋅ (v0 ⋅ sinα) ⋅ B = m ⋅ (v^2)/r

Da tale relazione si ricava il raggio dell'elica:

r = m ⋅ (v0 ⋅ sinα)/qB

Trattandosi di un moto elicoidale, si può conoscere la componente della velocità angolare ω. In particolare, essendo valida la seguente relazione:

v ⋅ sin(α) = ω ⋅ r

si ha che:

ω = (q ⋅ B)/m

Utilizzando le leggi del moto periodico, è inoltre possibile conoscere il periodo T del fascio, che indica il tempo impiegato per percorrere una volta la circonferenza, tramite la seguente relazione.

T = (2π ⋅ m)/e ⋅ B

Componente della velocità parallela a B

Invece, andando ad analizzare la componente parallela del vettore velocità degli elettroni, si nota come nessuna forza agisca su di essi, dato che la forza di Lorentz dipende dal seno dell'angolo tra la velocità e il campo magnetico B e, analizzando la componente parallela della velocità, tale angolo è di 0 gradi.

Si può quindi analizzare solo la distanza che viene percorsa parallelamente al campo magnetico in un periodo T: tale grandezza è il passo dell'elica e viene determinata dalla seguente relazione:

p = v ⋅ cos(α) ⋅ T

Che è a sua volta equivalente a

p = (2π ⋅ m) ⋅ v ⋅ cos(α)/q ⋅ B

SELETTORE DI VELOCITA'

Usando il selettore di velocità, possiamo facilmente trovare delle particelle con una data carica specifica

Impostiamo così:

il selettore di velocità è un dispositivo che unisce un campo elettrico e un campo magnetico a esso perpendicolare. Le piastre del condensatore producono un campo elettrico posto in un campo magnetico. Alla fine delle piastre c'è un'apertura. Così solo le particelle, che si muovono nel mezzo del dispositivo possono passare il selettore di velocità.

Il fascio di elettroni entra nel selettore di velocità con una velocità il cui vettore è perpendicolare al campo elettrico e al campo magnetico

Funzione

Quando gli elettroni entrano nel selettore di velocità, il campo magnetico e quello elettrico generano due forze diverse. il campo elettrico genera la forza elettrica (forza di Coulomb):

Fel = q ⋅ E

il movimento degli elettroni all'interno del campo magnetico genera la forza di Lorentz:

FLorentz = q ⋅ v ⋅ B

solo le particelle la cui velocità può essere calcolata equiparando le due forze avrà la traiettoria necessaria per poter uscire dall'apertura:

Fel = FLorentz

q ⋅ E = q ⋅ v ⋅ B

semplificando l'espressione e isolando la velocità, si ricava

vpassaggio = E/B

Se la velocità degli elettroni è maggiore di v(passaggio), si deduce che la FLorentz è più grande di Fel.

Se la velocità degli elettroni è minore di v(passaggio), si deduce che la FLorentz è più piccola di Fel.

Limitazioni:

per capire se un elettrone passa attraverso l'apertura, bisogna calcolare la sua velocità, mentre la sua carica e la sua massa non influiscono.

SPETTROMETRO DI MASSA

Un selettore di velocità consente di isolare le particelle che hanno una velocità specifica da un fascio. Per investigare la massa delle particelle è necessario estendere la configurazione dell'esperimento. Una configurazione utile per esaminare la massa delle particelle è lo spettrometro di massa Bainbridge.

Seguiamo la seguente impostazione:

nella configurazione più estesa, il campo magnetico non finisce in corrispondenza dell'apertura. Quindi, dopo aver passato il selettore di velocità, la particella rimane nel campo magnetico. Lì la forza di Lorentz è l'unica forza che influenza il movimento delle particelle, le quali pertanto inizieranno a muoversi di moto circolare. Oltre alla configurazione del selettore di velocità c'è quindi una piastra di rilevamento sul retro dell'apertura. Questa piastra rileva il punto nel quale le particelle vanno a sbattere.

Funzione

Se una particella si muove con velocità v in presenza di un campo magnetico B, allora subirà una forza di Lorentz perpendicolare alla direzione del moto:

FLorentz = q ⋅ v ⋅Bsin(α)

Questa forza fa sì che le particelle inizino a muoversi di moto circolare in quanto la F Lorentz agisce come F centripeta sulle particelle, il raggio r risulta quindi:

FLorentz = Fcentripeta

q ⋅ v ⋅ B = m ⋅ v^2/r

r = m ⋅ v/q ⋅ B

A causa del selettore di velocità tutte le particelle hanno la velocità v = vpassaggio, la quale a sua volta è uguale a E/B.

Segue che:

r = (m ⋅ vpassaggio)/q ⋅ B

E pertanto r = (m ⋅ E)/q ⋅ B^2

Quindi possiamo affermare che particelle con uguale carica e massa si muovono su percorsi circolari con raggio diverso.

Pertanto andranno a collidere con lo schermo in differenti posizioni. In particolar modo con la distanza d = 2r tra il punto di impatto e l'apertura del selettore di velocità, la massa delle particelle può essere calcolata con:

m= (q ⋅ B ⋅ d) / 2 ⋅ (vpassaggio), ovvero m = (q ⋅ d ⋅ B^2)/2E

Limitazioni:

Con uno spettrometro di massa Bainbridge è possibile esaminare solo le particelle cariche, quindi le particelle non cariche devono essere caricate come prima cosa. Inoltre la carica deve essere nota per calcolare la massa delle particelle, altrimenti può essre calcolata solo la carica specifica g/m. 

Particelle con lo stesso impatto massa-carica-raggio impattano sullo schermo del rivelatore alla stessa distanza dall’apertura.

CONFIGURAZIONE CICLOTRONE

Configurazione:

Le parti principali di un ciclotrone sono elettrodi di metallo a forma di D chiamati "Dees" (più semplicemente li chiameremo elettrodi). Tra i due elettrodi vi è un'alta differenze di potenziale. Il potenziale va a caricare i due elettrodi, uno positivamente e uno negativamente. Sopra e sotto questi elettrodi sono posti degli elettromagneti forti, che producono un campo magnetico perpendicolare alla traiettoria degli elettroni. In uno dei due elettrodi è posizionata una sorgente di carica, la quale permette agli elettroni di superare il vuoto tra i due elettrodi.

Funzione di un ciclotrone

I protoni emessi dalla sorgente T hanno una velocità iniziale v0 quando sono posti nello spazio tra i due elettrodi. Se l'elettrodo uno è carico positivamente e l'elettrodo due negativamente, le particelle sono accelerate nello spazio tra i due elettrodi per effetto del campo elettrico. In seguito, quando le particelle entrano all'elettrodo uno, esse abbandonano il campo elettrico. All'elettrodo si può trovare un campo magnetico perpendicolare all'elettrodo stesso, quindi la forza di Lorentz agisce sulle particelle, generando una traiettoria circolare. mentre gli elettroni si trovano su un elettrodo, gli elettroni cambiano la propria carica, invertendo così il verso del campo elettrico; quindi dopo aver compiuto un semicerchio gli elettroni sono accelerati, trovandosi di nuovo nello spazio tra i due elettrodi. Nell'elettrodo 2 la forza di Lorentz genera una traiettoria circolare per i protoni di raggio maggiore a quella precedente. Pertanto, viene aumentata sia la traiettoria che la velocità.

dopo numerosi passaggi tra i due elettrodi la velocità dei protoni diventa vicina al 10% della velocità della luce.

Limitazioni

Questo tipo di ciclotrone può essere utilizzato per aumentare la velocità delle particelle fino a "solamente" il 10% della velocità della luce. Quando le particelle diventano più veloci vanno considerati gli effetti della relatività. A causa di questa limitazione sono accelerate grazie a questo tipo di ciclotrone solamente particelle pesanti come protoni e deuteroni; la tensione di accelerazione, dopo 50 transizioni circolari tra un elettrodo e l'altro, corrisponde a 10 MeV.

Calcolo della frequenza del ciclotrone

La forza di Lorentz equivale alla forza centripeta e muoverà le particelle di una traiettoria circolare:

FLorentz = Fcentripeta

q ⋅ v ⋅ B = m ⋅ v^2/r

v = r ⋅ q ⋅ B/m

Con v = ω ⋅ r = 2π ⋅ f ⋅ r

2π ⋅ f ⋅ r = r ⋅ q ⋅ B/m

f = q ⋅ B/2π ⋅ m

È il periodo coincide con:

T = 1/f = 2π ⋅ m/q ⋅ B

La frequenza del ciclotrone f, il periodo e quindi il tempo che una particella impiega per sorpassare un elettrodo non dipende dal raggio r. Così è possibile mantenere la frequenza della differenza di potenziale costante.

L'energia cinetica cresce ad ogni passaggio delle particelle tra lo spazio vuoto tra i due elettrodi di q V

Ecin(n) = Ecin0 + n ⋅ q ⋅V = ½m ⋅ v0^2 + n ⋅ q ⋅V

La velocità v delle particelle può essere calcolata partendo dalla velocità iniziale v0 che esse hanno quando abbandonano la sorgente e dal numero n si passaggi nel vuoto tra i due elettrodi:

½ ⋅ m ⋅ v^2 = ½ m ⋅ v0^2 + n ⋅ q ⋅ V

v = √( 2/m ) ⋅ ( ½m ⋅ v0^2 + q ⋅ V ⋅ n)

Se la velocità iniziale coincide a 0, v0 = 0

Si può ricorrere alla seguente formula:

v = √2/m ⋅ q ⋅ V ⋅ n