DEFLESSIONE ELETTRICA
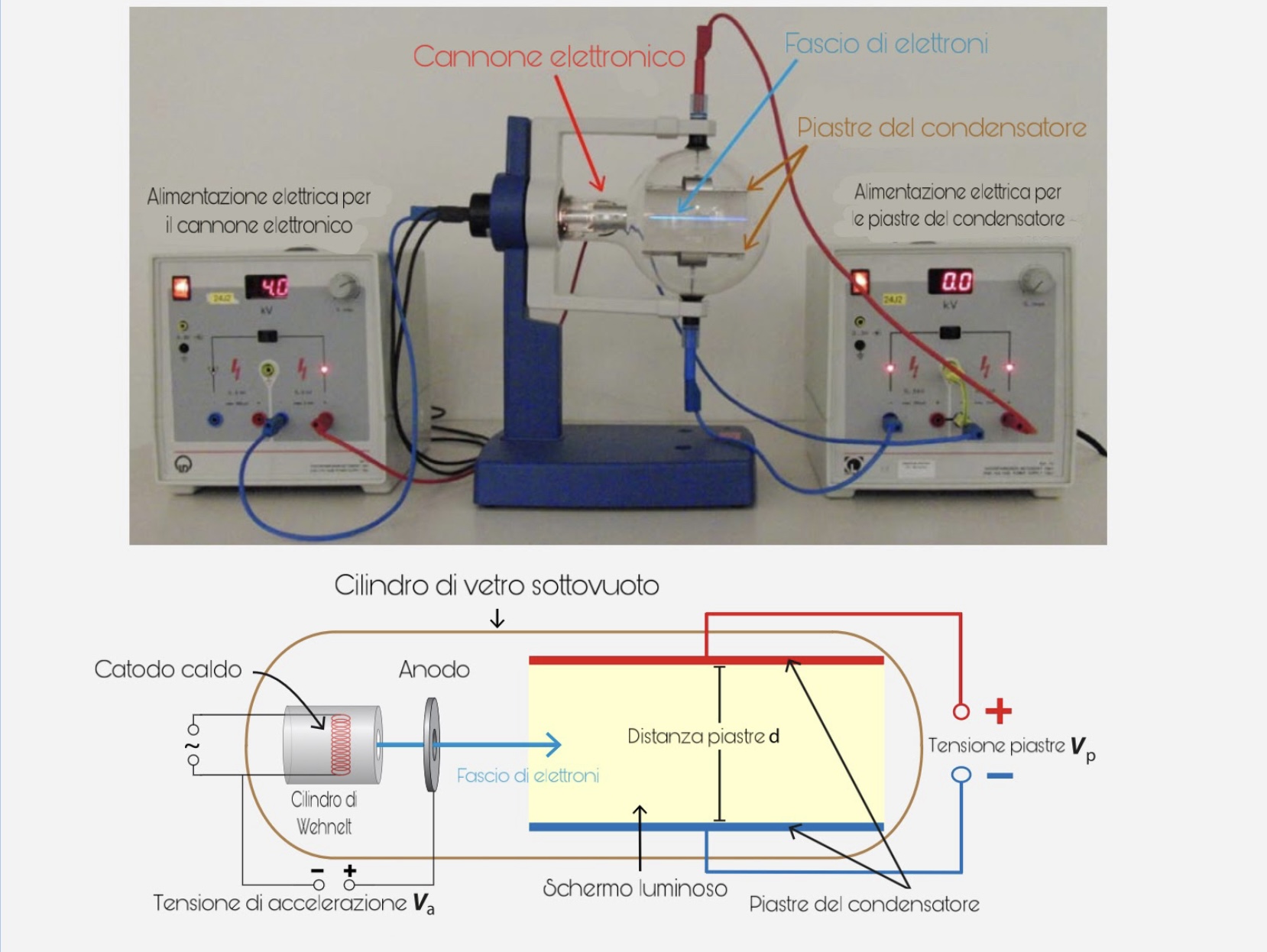
Quale è l'effetto di un campo elettrico sul moto degli elettroni?
Quale è la traiettoria degli elettroni in un condensatore a piastre?
Viene utilizzata la seguente configurazione: un cannone elettronico in un tubo di vetro produce un fascio di elettroni. Questo fascio entra perpendicolarmente al campo elettrico di un condensatore a piastre, dove uno schermo luminoso mostra la traiettoria degli elettroni. Gli elettroni si muovono su uno schermo rivestito di una sostanza fluorescente che ne rende visibile la traiettoria.
IPOTESI
Guardando la seconda immagine, si può affermare che la tensione di accelerazione del cannone elettronico e la tensione del condensatore influenzano la traiettoria dell'elettrone. In particolar modo, all'aumentare della tensione del condensatore (Vp) la deflessione della traiettoria dell'elettrone aumenta, andando a scontrarsi con una piastra del condensatore. Al contrario, all'aumentare della tensione di accelerazione (Va) la deflessione della traiettoria diminuisce. Per analogia, all'aumentare della forza del campo elettrico tra le due piastre aumenta la deflessione della traiettoria dell'elettrone, all'aumentare di v0, invece, diminuisce la deflessione della traiettoria (vedi immagine al paragrafo: “forma della curva").
ESPERIMENTO
Tensione del condensatore
Per la deflessione degli elettroni vale: quanto più maggiore è Vp, tanto la deflessione y(x) è maggiore.
Obiettivo: verificare se abbiamo anche Y(x) ~ Vp

Per il controllo la tensione di accelerazione Va è impostata a 3,5 kV .
Poiché il rapporto y(x)/Vp è approssimativamente costante, la deflessione y(x) risulta proporzionale alla tensione del condensatore Vp.
Abbiamo quindi verificato che Y(x) ~ Vp
Influenza della distanza tra le piastre del condensatore sulla traiettoria
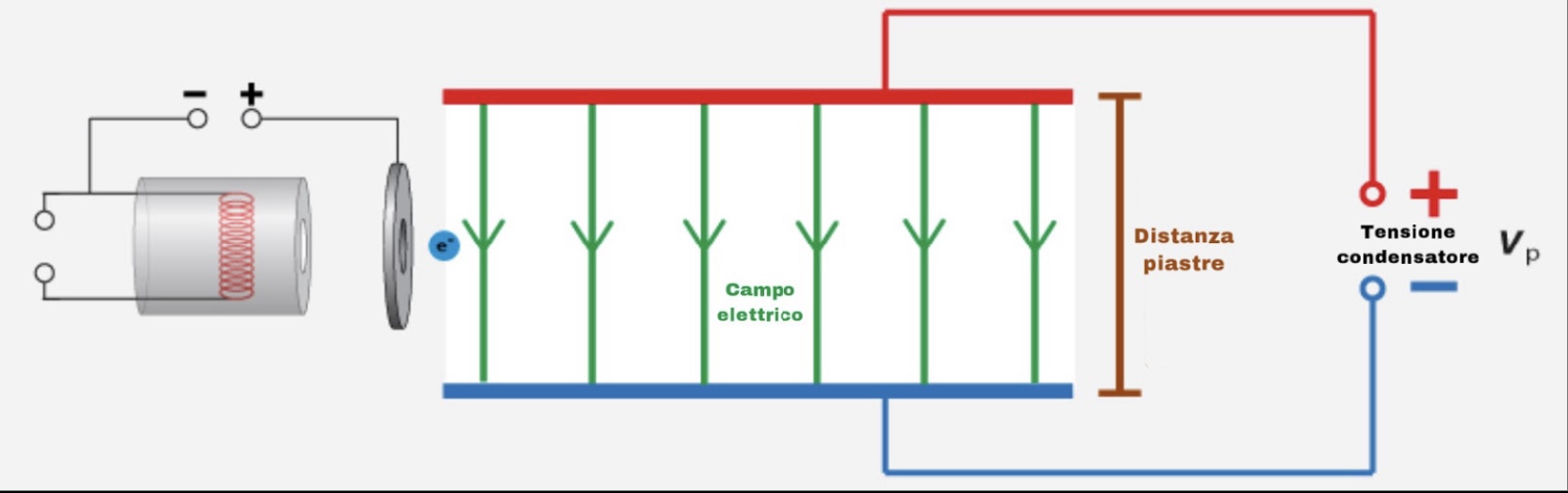
Considerando il campo elettrico generato dal condensatore, la distanza d tra le due piastre è inversamente proporzionale alla forza del campo elettrico tra le piastre; in quanto:
E = Vp/d
inoltre, nel nostro esperimento la distanza è costante, quindi si può così affermare:
y(x) ~ Vp/d
di conseguenza y(x) ~ E
In particolare, nel tubo di deflessione degli elettroni utilizzato nel nostro studio la distanza d tra le piastre del condensatore è uguale a 5.4 cm .
Tensione di accelerazione
Per le precedenti ipotesi, minore è la Va, maggiore è la deflessione Y(x).
Obiettivo: verificare se anche Y(x) è inversamente proporzionale a Va.
Per farlo abbiamo posto Va uguale a 3,2 kV.
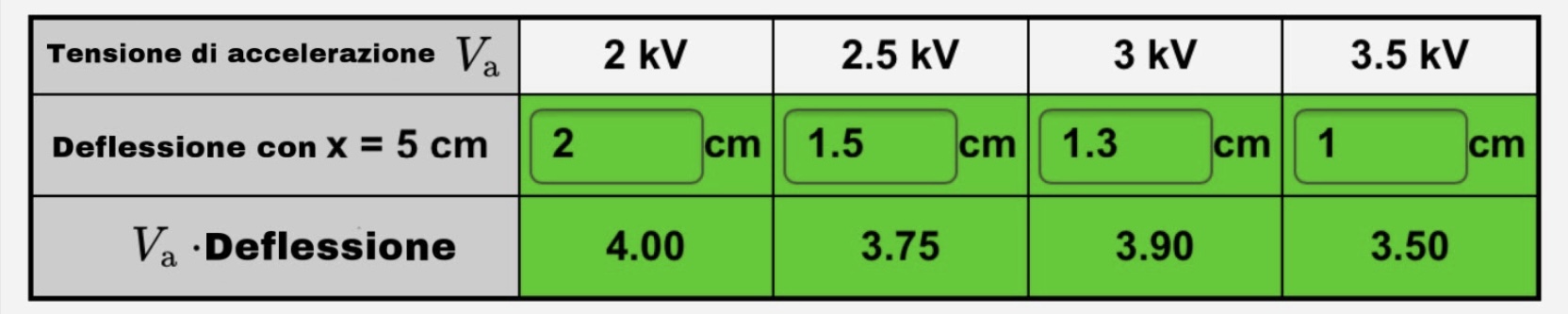
Si nota che il prodotto Va ⋅ Y(x) è approssimativamente costante, pertanto abbiamo verificato:
Y(x) ~ 1/Va
Forma della curva
Andiamo ora a riportare i dati precedentemente ottenuti per analizzare la forma della traiettoria compiuta degli elettroni.

Con la formule ricavate andiamo a creare la funzione che descrive il moto del fascio di elettroni.
Precedentemente abbiamo ottenuto le seguenti formule:
y(x) ~ Vp/d
y(x) ~ 1/Va
y(x) ~ x^2
Mettendole a sistema si può ricavare la funzione generale dell’andamento del fascio:
y(x) = ¼ ⋅ Vp/d ⋅ 1/Va ⋅ x^2
Ne consegue quindi che y(x) = (Vp ⋅ x^2)/(4 ⋅ d ⋅ Va)
Tale funzione descrive una parabola allungata o compressa che può essere visualizzata nella seguente immagine:
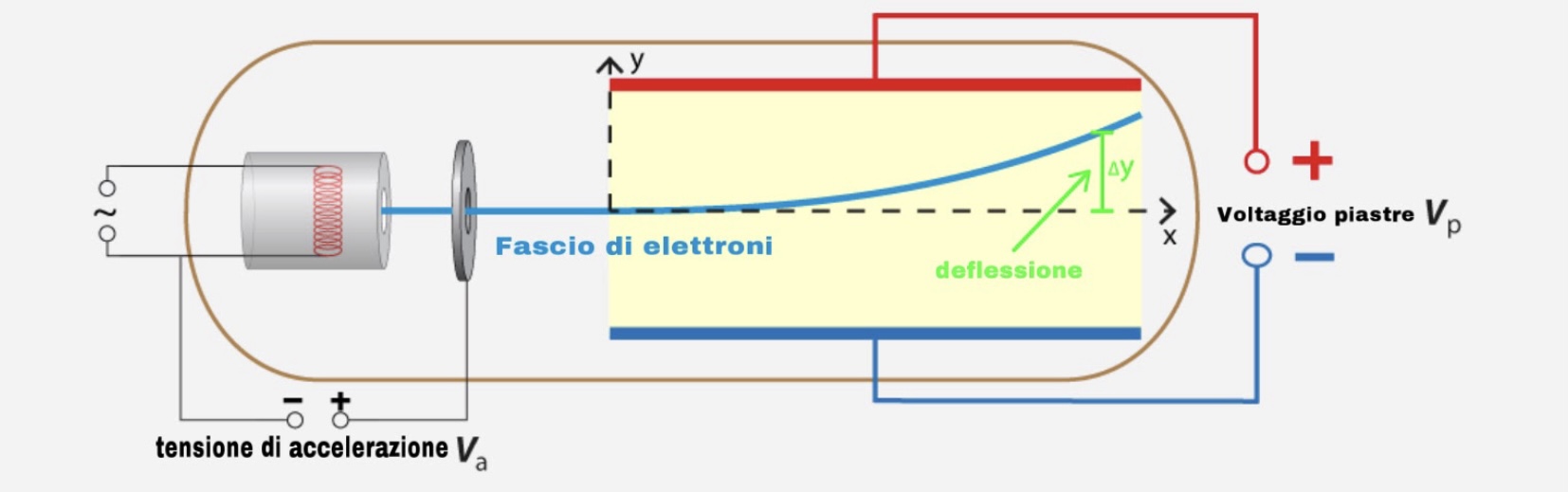
FORZE E EQUAZIONI DEL MOTO
Andiamo ora ad analizzare le forze agenti e le equazioni del moto derivanti.
In particolare, tra le piastre del condensatore ci sono delle forze che agiscono sul fascio di elettroni:
- lungo la direzione orizzontale non agisce nessuna forza, quindi gli elettroni compiono una traiettoria lineare;
- lungo la direzione verticale agisce una forza che è costante, generando quindi un'accelerazione, anch'essa costante, in questa direzione.
Le equazioni del moto sull'asse x sono:
- x(t) = v0 ⋅ t
- vx(t) = v0
- ax(t) = 0
Le equazioni del moto sull’asse y sono:
- y(t) = ½ ⋅ ay ⋅ t^2
- vy(t) = ay ⋅ t
- ay(t) = F/m = (Vp ⋅ e)/(m ⋅ d)
Per calcolare un'equazione che descriva il percorso dell’ elettrone, è necessario sostituire il tempo t, ricavato dalla legge oraria della direzione x, nella legge oraria della direzione y.
Ricaviamo quindi la seguente formula:
y(x) = (ay ⋅ x^2)/(2 ⋅ v0^2)
Sostituendo nella formula appena ottenuta, l’accelerazione definita dal secondo principio della dinamica (F= m a) si ottiene, in direzione y:
ay(t) = (Up ⋅ e)/(d ⋅ m)
Ricaviamo quindi la formula:
y(x) = (Vp ⋅ e ⋅ x^2)/ (2 ⋅ d ⋅ m ⋅ v0^2)
sostituendo v0 con formula v0 = √(2 ⋅ e ⋅ Ub/m)
otteniamo la formula: y(x) = (Up ⋅ x^2)/(4 ⋅ d ⋅ Ub)
ANALOGIA CON IL LANCIO ORIZZONTALE DEL PROIETTILE
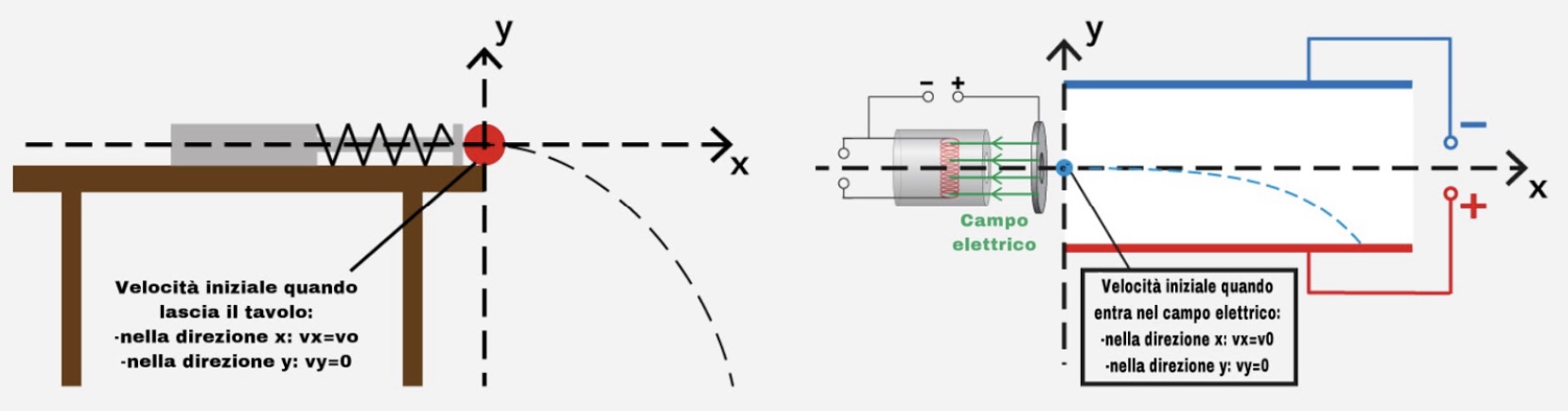
1. MOTO DEL PROIETTILE 2. MOTO DEL FASCIO DI ELETTRONI
Velocità iniziale
1. Per calcolare la v0 iniziale nel moto di caduta di un oggetto bisogna equiparare l’equazione dell’energia dell’energia potenziale elastica (della molla):
Ue = ½ ⋅ k ⋅ x^2
all’energia cinetica:
Ec = ½ ⋅ m ⋅ v^2
così otteniamo v0 isolandola:
v0 = √((k/m) ⋅ s)
2. Mentre per calcolare la v0 nel tubo di deflessione del fascio di elettroni bisogna equiparare l’equazione del lavoro del campo elettrico E:
L = Va ⋅ e
all’energia cinetica degli elettroni
Ec = ½ ⋅ m ⋅ v^2
così otteniamo v0 isolandola:
v0 = √(2 ⋅ e ⋅ Va/m)
Direzione orizzontale
1. Dopo aver lasciato il cannone non ci sono forze che accelerano la massa nella direzione
orizzontale, di conseguenza possiamo utilizzare le seguenti formule:
x(t) = v0 ⋅ t
v = v0
a = 0
2. Dopo aver lasciato il cannone ad elettroni non ci sono forze che accelerano gli elettroni nella
direzione orizzontale, di conseguenza possiamo utilizzare le seguenti formule:
x(t) = v0 ⋅ t
v = v0
a = 0
Direzione verticale
1. Dopo aver lasciato il tavolo, la forza gravitazionale accelera la massa in direzione verticale, di
conseguenza possiamo utilizzare le seguenti formule:
y(t) = ½ ⋅ ay ⋅ t^2
v(t) = ay ⋅ t
ay = -g
2. Dopo essere entrato nel campo elettrico del condensatore, la forza elettrica accelera gli elettroni
in direzione verticale, di conseguenza possiamo utilizzare le seguenti formule:
y(t) = ½ ⋅ ay ⋅ t^2
v(t) = ay ⋅ t
ay = -E ⋅ e/m
ovvero ay = -Vp ⋅ e/(d ⋅ m)
Traiettoria
1. L’equazione per calcolare la traiettoria di un oggetto lanciato orizzontalmente equivale a:
y(x) = -½ ⋅ (g ⋅ m ⋅ x^2)/(K ⋅ d^2)
2. L’equazione per calcolare la traiettoria di un elettrone che fuoriesce dal cannone ad elettroni
equivale a:
y(x) = -¼ ⋅ (Vp ⋅ x^2)/(d ⋅ Va)
MOVIMENTO DOPO IL CAMPO ELETTRICO
Angolo d’uscita
Per calcolare l’angolo d’uscita di un elettrone dal campo elettrico bisogna utilizzare l’equivalenza:
tan(α) = vy/vx
pertanto l’angolo si calcola come:
α = arctan(vy/vx)
Traiettoria
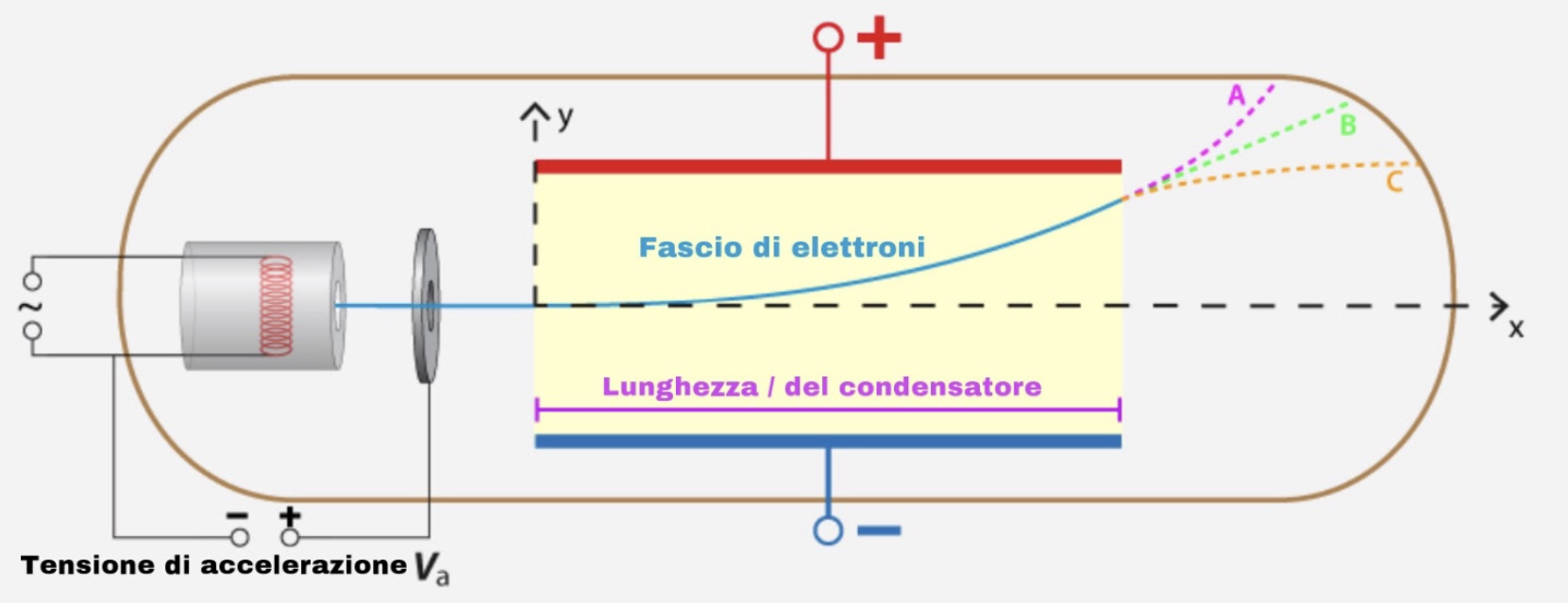
Quando gli elettroni lasciano le piastre del condensatore abbandonano anche il campo elettrico, pertanto nessuna forza agisce sugli elettroni, quindi le velocità vx e vy sono costanti e gli elettroni seguono il percorso B muovendosi di moto rettilineo uniforme.
Impatto sullo schermo
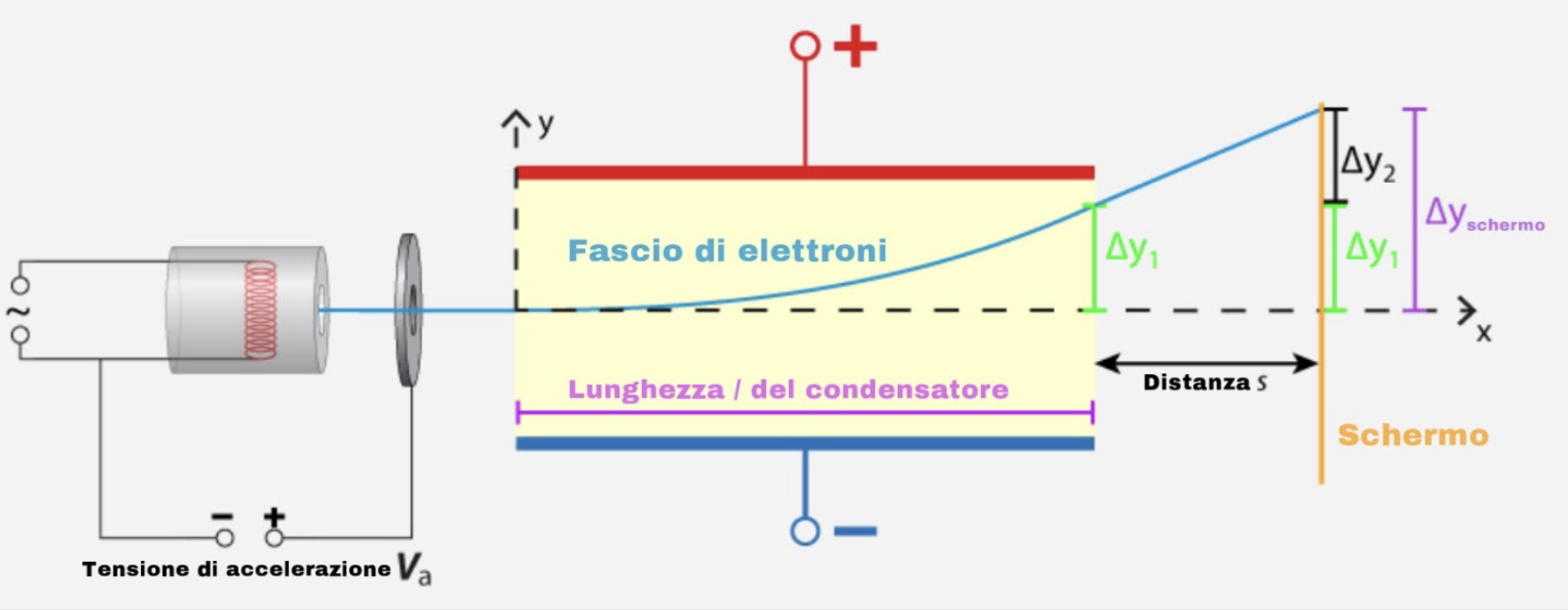
Supponendo che gli elettroni impattino su uno schermo possiamo calcolare la deflessione Δyschermo .
La deflessione Δy2 = vy⋅ t
dove t = s/vx
di conseguenza la deflessione Δyschermo = Δy1 + vy ⋅ s/vx
